Artificial intelligence (AI) is emerging as one of the key industry trends after decades of just being a researcher’s dream. From conversations with Alexa and Siri to Waymo (Google) and Tesla’s vehicles driving themselves, OpenAI’s GPT-3 writing prose like a human, and DeepMind (Google)’s AlphaZero beating human chess grandmasters, it is becoming clear that AI is now mature enough to resolve real-life problems and is often faster and better at it than humans.
Elsewhere in the tech industry, several visionaries are working towards developing quantum computers, which seek to leverage the properties of quantum physics to perform calculations much faster than today’s computers.
At this point, you cannot be blamed for wondering: what exactly has quantum computing got to do with AI?
Algorithmic complexity is the hidden enemy
Algorithmic complexity is a somewhat obscure mathematical concept that connects the work being done by AI researchers and quantum computing pioneers.
Computational complexity theory, a field sitting across mathematics and computer science, focuses on classifying computational problems according to their resource usages, such as space (memory) and time. In essence, a computational problem is a task that can be solved by a computer mechanically following the mathematical steps defined in an algorithm.
For instance, consider the problem of sorting the numbers in a list. One possible algorithm, called ‘Selection Sort’, consists of repeatedly finding the minimum element (in ascending order) from the unsorted part of the list (initially, all of it) and putting it at the beginning. This algorithm effectively maintains two sub-lists within the original list as it works its way through: the already sorted part and the remaining unsorted part. After several passes of this process, the outcome is a sorted list from smaller to larger. In terms of time complexity, this is expressed by the complexity of N2, where N means the size or number of elements in the list. Mathematicians have come up with more efficient, albeit more complex sorting algorithms, such as ‘Cube Sort’ or ‘Tim Sort’, both of which have an N x log(N) complexity. Sorting a list of 100 elements is a simple task for today’s computers but sorting a list of a billion records might be less so. Therefore, the time complexity (or the number of steps in the algorithm in relation to the size of the input problem) is very important.
How well do you really know your competitors?
Access the most comprehensive Company Profiles on the market, powered by GlobalData. Save hours of research. Gain competitive edge.

Thank you!
Your download email will arrive shortly
Not ready to buy yet? Download a free sample
We are confident about the unique quality of our Company Profiles. However, we want you to make the most beneficial decision for your business, so we offer a free sample that you can download by submitting the below form
By GlobalData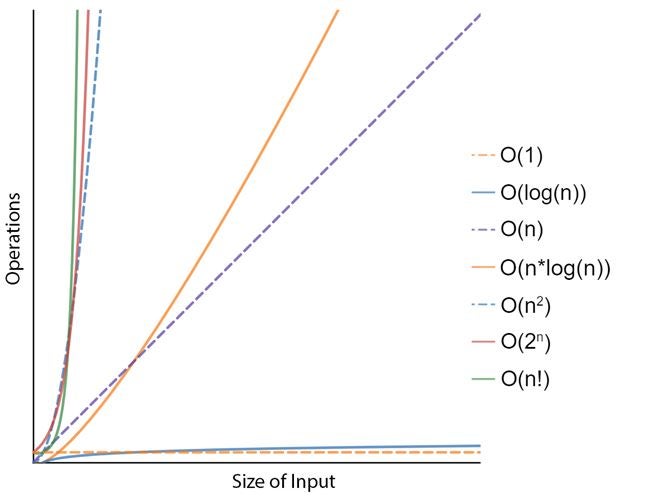
To solve a problem faster, one can either use a faster computer or find a more efficient algorithm that requires fewer operations, which is what lower time complexity means. However, it is clear that in the case of problems of exponential complexity (for instance, N2 or 2N), the math works against you, and with larger problem sizes it is not realistic to just use faster computers. And this is precisely the case in the field of artificial intelligence.
AI is a highly complex problem to solve
First, we will look at the computational complexity of the artificial neural networks used by today’s artificial intelligence (AI) systems. These mathematical models are inspired by the biological neural networks that constitute animal brains. They ‘learn’ to identify or categorize input data, by seeing many examples. They are a collection of interconnected nodes or neurons, combined with an activation function that determines the output based on the data presented in the ‘input layer’ and the weights in the interconnections.
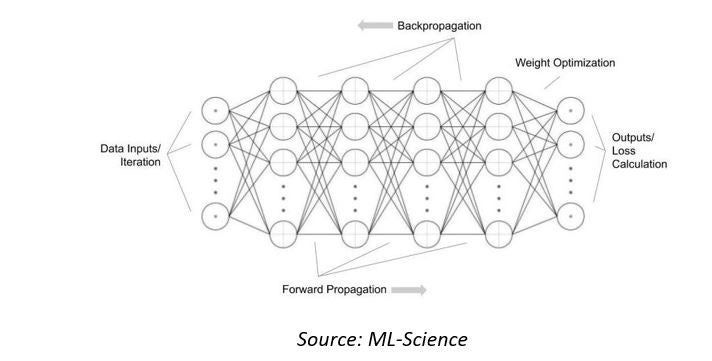
To adjust the weights in the interconnections so that the ‘output’ is useful or correct, the network can be ‘trained’ by exposure to many data examples and ‘backpropagating’ the output loss.
For a neural network with N inputs, M hidden layers, where the i-th hidden layer contains mi hidden neurons, and k output neurons, the algorithm that adjusts the weights of all neurons (called a backpropagating algorithm) will have a time complexity of:
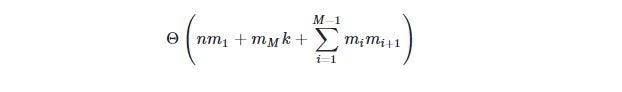
To put things in context, the popular OpenAI’s GPT-3 model, which is already capable of writing original prose with fluency equivalent to that of a human, has 175 billion parameters (or neurons). With an M in the billions, this AI model currently takes months to train, even using powerful server computers in large cloud data centers. Furthermore, AI models are going to continue growing in size, so the situation will get worse over time.
Quantum computing to the rescue?
Quantum computers are machines that use the properties of quantum physics, specifically superposition and entanglement, to store data and perform computations. The expectation is that they can execute billions of simultaneous operations, therefore providing a very material speedup for highly complex problems, including AI.
While classical computers transmit information in bits (short for ‘binary digits’), quantum computers use qubits (short for ‘quantum bits’). Like classical bits, qubits do eventually have to transmit information as a one or zero but are special in that they can represent both a one and a zero at the same time. A qubit is considered to have a probability distribution, e.g., it is 70% likely to be a one and 30% likely to be a zero. This is what makes quantum computers special.
There are two essential properties in quantum mechanics that quantum computers take advantage of: superposition and entanglement.
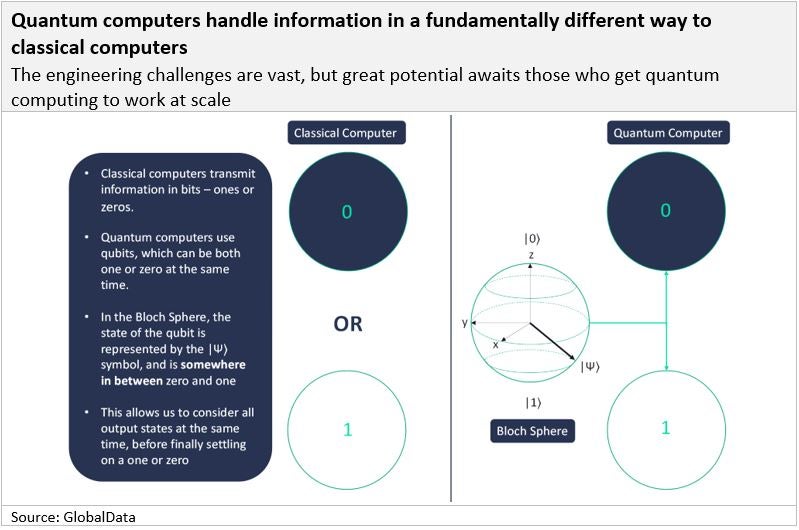
When a qubit is both a one and a zero at the same time, it is said to be in a superposition. Superposition is the general name for the condition when a system is in multiple states at once and only assumes a single state when it is measured. If we pretend that a coin is a quantum object, a superposition can be imposed when the coin is flipped: there is only a probability of the coin being either heads or tails. Once the coin has landed, we have made a measurement, and we know whether the coin is heads or tails. Likewise, only when we measure the spin of an electron (similar to the coin landing) do we know what state the electron is in and whether it is a one or a zero.
Quantum particles in superposition are only useful if we have more than one of them. This brings us to our second fundamental principle of quantum mechanics: entanglement. Two (or more) particles that are entangled cannot be individually described, and their properties depend completely on one another. So, entangled qubits can affect each other. The probability distribution of a qubit (being a one or zero) depends on the probability distribution of all other qubits in the system.
Because of that, the addition of each new qubit to a system has the effect of doubling the number of states that the computer can analyze. This exponential increase in computer power contrasts with classical computing, which only scales linearly with each new bit.
Entangled qubits can, theoretically, execute billions of simultaneous operations. It is obvious that this capability would provide a dramatic speedup to any algorithm with complexities in the range of N2, 2N, or NN.
Getting ready for quantum-powered AI
Because of the impressive potential of quantum computing, while hardware teams continue to work on making these systems a reality (the largest to date is IBM’s 127-Qubit Eagle system), software researchers are already working on new algorithms that could leverage this ‘simultaneous computation’ capability, in fields such as cryptography, chemistry, materials science, systems optimization, and machine learning/AI. It is believed that Shor’s factorization quantum algorithm will provide an exponential speedup over classical computers, which poses a risk to current cryptographic algorithms.
Most interestingly, it is believed quantum linear algebra will provide a polynomial speed-up, which will enormously improve the performance of our artificial neural networks. Google has launched TensorFlow Quantum, a software framework for quantum machine learning, which allows rapid prototyping of hybrid quantum-classical ML models. IBM, also a leader in quantum computing, recently announced that it has found “mathematical proof” of a quantum advantage for quantum machine learning. However, while the likes of IBM and Google are vertically integrated (thus developing both the hardware systems and the software algorithms) there is also a very interesting group of quantum software start‑ups including Zapata, Riverlane, 1Qbit, and, to a certain degree, Quantinuum (since Cambridge Quantum Computing merged with Honeywell and rebranded, it is not a pure software company anymore), to name just a few.
As quantum hardware becomes more powerful and quantum machine learning algorithms are perfected, quantum computing is likely to take a significant share of the AI chips market. For a more detailed discussion on AI chips and quantum computing, please take a look at our thematic reports on AI, AI chips, and quantum computing.








Related Company Profiles
Tesla Inc
Waymo LLC